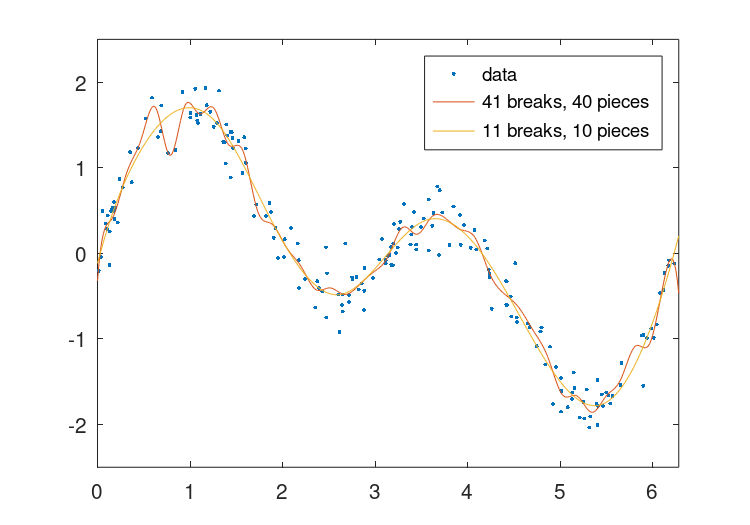
图28.1:具有41个断点的分段多项式与具有11个断点的多项式的拟合的比较。具有大量断裂的拟合表现出快速的波纹,这在基础函数中是不存在的。
Octave为各种插值提供了良好的支持,其中大部分在中进行了描述Interpolation上述章节中描述的函数的一个简单替代方案是将单个多项式或分段多项式(样条曲线)拟合到一些给定的数据点。为了避免高度波动的多项式,人们通常希望将低阶多项式拟合到数据中。这通常意味着在最小二乘意义上拟合多项式是必要的,这就是polyfit函数确实如此。
用于计算多项式效率的范德蒙矩阵。
来自QR分解的三角因子R。
未缩放的协方差矩阵,形式上等于的倒数x’*x,但是以最小化舍入误差传播的方式进行计算。
自由度。
残差的范数。
第二输出可从polyval以计算预测值的统计误差极限。特别是的标准偏差p系数从
sqrt (diag (s.C)/s.df) * s.normr.
当第三输出,mu,对原始数据进行了居中和缩放,这可以提高拟合的数值稳定性。系数p与中的多项式相关联
xhat = (x - mu(1)) / mu(2)
这里的mu(1) =平均值(x和mu(2) =标准(x).
示例1:逻辑n和整数n
f = @(x) x.^2 + 5; # data-generating function x = 0:5; y = f (x); ## Fit data to polynomial A*x^3 + B*x^1 p = polyfit (x, y, logical ([1, 0, 1, 0])) ⇒ p = [ 0.0680, 0, 4.2444, 0 ] ## Fit data to polynomial using all terms up to x^3 p = polyfit (x, y, 3) ⇒ p = [ -4.9608e-17, 1.0000e+00, -3.3813e-15, 5.0000e+00 ]
详见: polyval, polyaffine, roots, vander, zscore.
在单个多项式不够好的情况下,解决方案是使用几个多项式拼凑在一起。函数splinefit将分段多项式(样条曲线)拟合到一组数据。
pp = splinefit (x, y, breaks) ¶pp = splinefit (x, y, p) ¶pp = splinefit (…, "periodic", periodic) ¶pp = splinefit (…, "robust", robust) ¶pp = splinefit (…, "beta", beta) ¶pp = splinefit (…, "order", order) ¶pp = splinefit (…, "constraints", constraints) ¶拟合带断点(节)的分段三次样条曲线breaks到那时的noisy数据,x和y.
x是一个向量,并且y是向量或N-D数组。如果y是一个N-D数组,那么x(j) 与匹配yj
p是一个正整数,定义沿x和p+1是中断次数。每个区间的点数相差不超过1。
可选属性periodic是一个逻辑值,用于指定周期边界条件是否应用于样条曲线。周期的长度为max (breaks) - min (breaks)。默认值为false.
可选属性robust是一个逻辑值,用于指定是否应用稳健拟合来减少输出数据点的影响。执行三次加权最小二乘迭代。权重是根据前一个残差计算得出的。外部识别的灵敏度从属性控制beta。的值beta被限制在范围内,0<beta1.默认值为beta= 1/2. 接近0的值赋予所有数据相等的权重。的值不断增加beta减少数据泄露的影响。接近1的值可能会导致不稳定或秩效率。
拟合的样条作为分段多项式返回,pp,可以使用进行评估ppval.
样条曲线是从次数为的多项式构成的order默认值为立方体,order=3.具有P个片的样条具有P+order自由度。在周期性边界条件下,自由度降为P。
可选属性,constraints,是一个在拟合上指定线性约束的结构体。该结构体具有三个字段,"xc","yc"和"cc".
"xc"约束的x位置的向量。
"yc"约束位置处的值xc。默认值是一个零数组。
"cc"系数(矩阵)。默认值是一个一的数组。行的数量被限制为分段多项式的阶数,order.
约束是0到的阶导数的线性组合order-1根据
cc(1,j) * y(xc(j)) + cc(2,j) * y'(xc(j)) + ... = yc(:,...,:,j).
详见: interp1, unmkpp, ppval, spline, pchip, ppder, ppint, ppjumps.
的数量breaks(或节点)是抑制输入数据中存在的噪声的重要因素,x和y。下面的例子说明了这一点。
x = 2 * pi * rand (1, 200);
y = sin (x) + sin (2 * x) + 0.2 * randn (size (x));
## Uniform breaks
breaks = linspace (0, 2 * pi, 41); % 41 breaks, 40 pieces
pp1 = splinefit (x, y, breaks);
## Breaks interpolated from data
pp2 = splinefit (x, y, 10); % 11 breaks, 10 pieces
## Plot
xx = linspace (0, 2 * pi, 400);
y1 = ppval (pp1, xx);
y2 = ppval (pp2, xx);
plot (x, y, ".", xx, [y1; y2])
axis tight
ylim auto
legend ({"data", "41 breaks, 40 pieces", "11 breaks, 10 pieces"})
其结果可以在中看到图28.1.

图28.1:具有41个断点的分段多项式与具有11个断点的多项式的拟合的比较。具有大量断裂的拟合表现出快速的波纹,这在基础函数中是不存在的。
分段多项式拟合,从提供splinefit,具有连续的导数,最高可达order-例如,一个三次fit具有连续的一阶导数和二阶导数。代码对此进行了演示
## Data (200 points)
x = 2 * pi * rand (1, 200);
y = sin (x) + sin (2 * x) + 0.1 * randn (size (x));
## Piecewise constant
pp1 = splinefit (x, y, 8, "order", 0);
## Piecewise linear
pp2 = splinefit (x, y, 8, "order", 1);
## Piecewise quadratic
pp3 = splinefit (x, y, 8, "order", 2);
## Piecewise cubic
pp4 = splinefit (x, y, 8, "order", 3);
## Piecewise quartic
pp5 = splinefit (x, y, 8, "order", 4);
## Plot
xx = linspace (0, 2 * pi, 400);
y1 = ppval (pp1, xx);
y2 = ppval (pp2, xx);
y3 = ppval (pp3, xx);
y4 = ppval (pp4, xx);
y5 = ppval (pp5, xx);
plot (x, y, ".", xx, [y1; y2; y3; y4; y5])
axis tight
ylim auto
legend ({"data", "order 0", "order 1", "order 2", "order 3", "order 4"})
其结果可以在中看到图28.2.
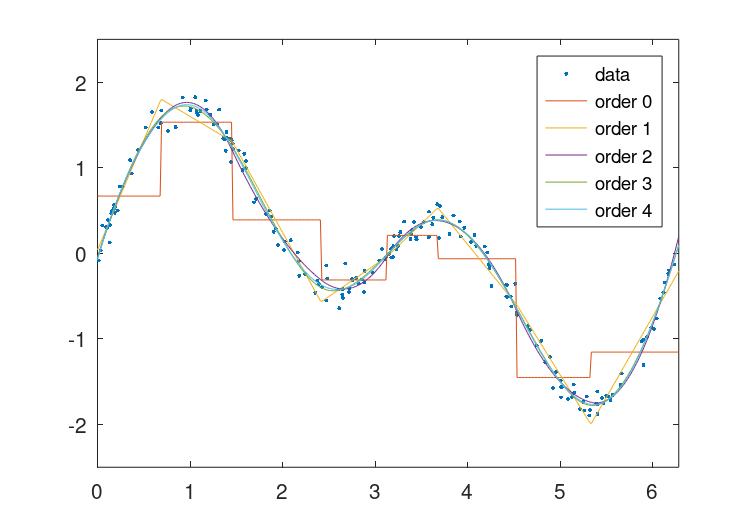
图28.2:具有8个中断的分段常数、线性、二次、三次和四次多项式与噪声数据的比较。高阶解更准确地表示底层函数,但也会带来计算复杂度的代价。
当提供拟合的基础函数是周期性的时,splinefit能够应用表现周期性拟合所需的边界条件。下面的代码演示了这一点。
## Data (100 points)
x = 2 * pi * [0, (rand (1, 98)), 1];
y = sin (x) - cos (2 * x) + 0.2 * randn (size (x));
## No constraints
pp1 = splinefit (x, y, 10, "order", 5);
## Periodic boundaries
pp2 = splinefit (x, y, 10, "order", 5, "periodic", true);
## Plot
xx = linspace (0, 2 * pi, 400);
y1 = ppval (pp1, xx);
y2 = ppval (pp2, xx);
plot (x, y, ".", xx, [y1; y2])
axis tight
ylim auto
legend ({"data", "no constraints", "periodic"})
其结果可以在中看到图28.3.
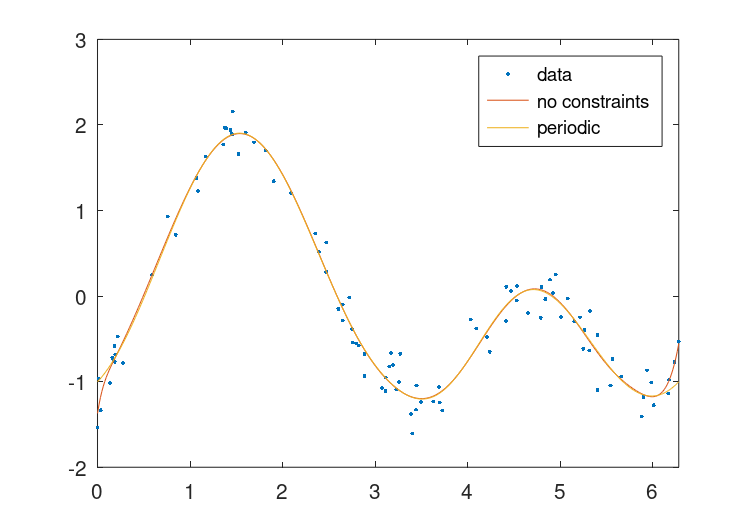
图28.3:分段多项式在有和无周期边界条件的情况下适用于有噪声的周期函数的比较。
也可以添加更复数的约束。例如,下面的代码将使用在端点处夹紧的值来计算一个周期性拟合,以及在端点处铰接的第二个周期性配合。
## Data (200 points)
x = 2 * pi * rand (1, 200);
y = sin (2 * x) + 0.1 * randn (size (x));
## Breaks
breaks = linspace (0, 2 * pi, 10);
## Clamped endpoints, y = y' = 0
xc = [0, 0, 2*pi, 2*pi];
cc = [(eye (2)), (eye (2))];
con = struct ("xc", xc, "cc", cc);
pp1 = splinefit (x, y, breaks, "constraints", con);
## Hinged periodic endpoints, y = 0
con = struct ("xc", 0);
pp2 = splinefit (x, y, breaks, "constraints", con, "periodic", true);
## Plot
xx = linspace (0, 2 * pi, 400);
y1 = ppval (pp1, xx);
y2 = ppval (pp2, xx);
plot (x, y, ".", xx, [y1; y2])
axis tight
ylim auto
legend ({"data", "clamped", "hinged periodic"})
其结果可以在中看到图28.4.
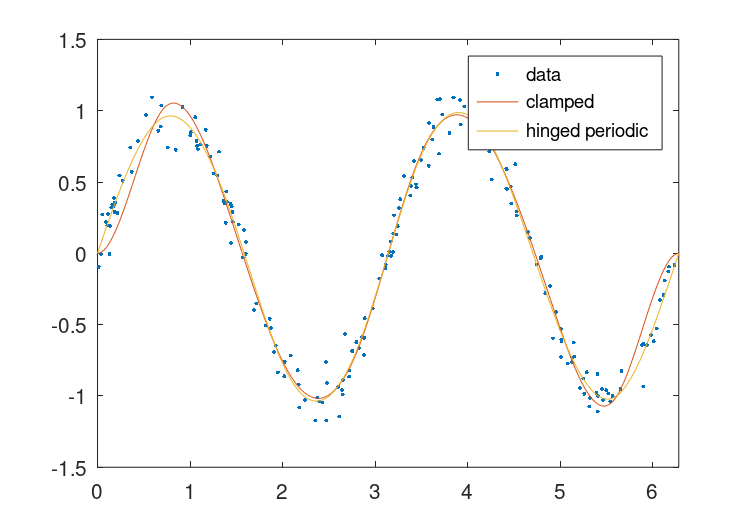
图28.4:两个周期分段三次拟合与噪声周期信号的比较。一个配合的端点被夹住,第二个配合的终点被磨光。
这里的splinefit函数还提供了robust拟合,其中减少了外围数据的影响。在下面的示例中,提供了三种不同的配合。两个具有不同的外部抑制水平,第三个说明了非鲁棒解决方案。
## Data
x = linspace (0, 2*pi, 200);
y = sin (x) + sin (2 * x) + 0.05 * randn (size (x));
## Add outliers
x = [x, linspace(0,2*pi,60)];
y = [y, -ones(1,60)];
## Fit splines with hinged conditions
con = struct ("xc", [0, 2*pi]);
## Robust fitting, beta = 0.25
pp1 = splinefit (x, y, 8, "constraints", con, "beta", 0.25);
## Robust fitting, beta = 0.75
pp2 = splinefit (x, y, 8, "constraints", con, "beta", 0.75);
## No robust fitting
pp3 = splinefit (x, y, 8, "constraints", con);
## Plot
xx = linspace (0, 2*pi, 400);
y1 = ppval (pp1, xx);
y2 = ppval (pp2, xx);
y3 = ppval (pp3, xx);
plot (x, y, ".", xx, [y1; y2; y3])
legend ({"data with outliers","robust, beta = 0.25", ...
"robust, beta = 0.75", "no robust fitting"})
axis tight
ylim auto
其结果可以在中看到图28.5.
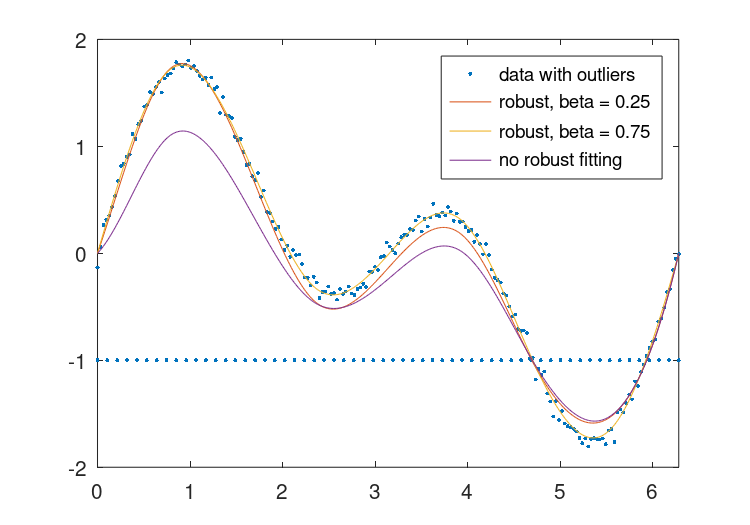
图28.5:两种不同稳健拟合水平的比较(beta=0.25和0.75)到与外围数据组合的噪声数据。传统合身,不合身(beta=0)。
一种非常具体的多项式解释形式是帕德近似。对于控制系统,连续时间延迟可以用近似值非常简单地建模。
[num, den] = padecoef (T) ¶[num, den] = padecoef (T, N) ¶计算N连续时滞的一阶Padé逼近T以传递函数的形式。
的Padé近似exp (-sT)从以下方程定义
Pn(s)
exp (-sT) ~ -------
Qn(s)
其中Pn(s)和Qn(s)都是N从以下表达式定义的次有理函数
N (2N - k)!N! k
Pn(s) = SUM --------------- (-sT)
k=0 (2N)!k!(N - k)!
Qn(s) = Pn(-s)
输入T和N必须是非负数字标量。如果N未指定,则默认为1。
输出行向量num和den包含以s的降序排列的分子和分母系数。两者都是N阶多项式。
例如
t = 0.1;
n = 4;
[num, den] = padecoef (t, n)
⇒ num =
1.0000e-04 -2.0000e-02 1.8000e+00 -8.4000e+01 1.6800e+03
⇒ den =
1.0000e-04 2.0000e-02 1.8000e+00 8.4000e+01 1.6800e+03
函数,ppval,计算分段多项式,从创建mkpp或其他方式,以及unmkpp返回有关分段多项式的详细信息。
以下示例显示如何将两个线性函数和aquadratic合并为一个函数。这些函数中的每一个都用邻接区间表示。
x = [-2, -1, 1, 2];
p = [ 0, 1, 0;
1, -2, 1;
0, -1, 1 ];
pp = mkpp (x, p);
xi = linspace (-2, 2, 50);
yi = ppval (pp, xi);
plot (xi, yi);
pp = mkpp (breaks, coefs) ¶pp = mkpp (breaks, coefs, d) ¶从采样点构造分段多项式(pp)结构体breaks和系数coefs.
breaks必须是值严格递增的向量。intervals的数量从ni = length (breaks) - 1.
当m是多项式阶coefs大小必须为:nixm1. .
的第i行coefs, coefs(i,:),包含多项式在i-第th个间隔,按最高顺序排列(m)至最低(0度
coefs也可以是多维数组,指定avector值或数组值多项式。在这种情况下,多项式阶m从的最后一个维度的长度定义coefs。第一个维度的大小从标量或向量给出d如果d未给定它设置为1.在这种情况下p(r, i, :)包含的系数r-区间上定义的第th个多项式i.无论如何coefs被变形为大小为2D的矩阵[ni*prod(d) m].
编程说明:ppval在处计算多项式xi - breaks(i),即从中减去当前间隔的下端xi。在创建具有mkpp.
[x, p, n, k, d] = unmkpp (pp) ¶提取分段多项式结构体的分量pp.
此函数与的相反mkpp:它提取输入到mkpp需要创建分段多项式结构体pp。下面的代码明确了这种关系:
[breaks, coefs, numinter, order, dim] = unmkpp (pp); pp2 = mkpp (breaks, coefs, dim);
分段多项式结构体pp2以这种方式获得,与原件不一样pp.同样可以通过直接访问结构体的字段来获得pp.
组件包括:
采样点或断点。
采样区间中点的多项式系数。p(i, :)包含多项式上区间的系数i从最高到最低排序。如果d > 1然后p是一个大小矩阵[n*prod(d) m],其中i + (1:d)行是所有的系数d区间中的多项式i.
多项式片段或区间的数量,n = length (x) - 1.
多项式的阶数加1。
为每个区间定义的多项式数。
yi = ppval (pp, xi) ¶评估分段多项式结构体pp在点上xi.
如果pp描述了一个标量多项式函数,结果是一个与相同形状的数组xi。否则,结果的大小为[pp.dim, length(xi)]如果xi是向量,或者[pp.dim, size(xi)]如果它是多维数组。
ppd = ppder (pp) ¶ppd = ppder (pp, m) ¶计算分段m-分段多项式结构体的th导数pp.
如果m则计算一阶导数。
ppi = ppint (pp) ¶ppi = ppint (pp, c) ¶计算分段多项式结构体的积分pp.
c,如果给定,则为积分常数。
jumps = ppjumps (pp) ¶评估分段多项式的边界跳跃。
如果有n区间,以及的维度pp是d,得到的数组具有维度[d, n-1].
详见: mkpp.
版权所有 © 2024-2025 Octave中文网
ICP备案/许可证号:黑ICP备2024030411号-2