22.4使用稀疏矩阵的实数生活示例¶
稀疏矩阵的一个常见应用是在有限元模型的求解中。有限元模型允许数值求解并没有闭合形式解的偏微分方程,这通常是因为域的形状很复数。
为了促进这一应用,我们考虑了边值拉普拉斯方程。这里的系统可以模拟标量势场,例如热或电势。给定一个具有边界dOmega的中等Omega。在dOmega上的所有点上,边界条件都是已知的,我们希望计算电势inOmega。边界条件可以指定势(Dirichlet边界条件)、其在边界上的法向导数(Neumann边界条件)或势与导数的加权和(Cauchy边界条件)。
在热模型中,我们想计算Omegaa中的温度,并知道边界温度(狄利克雷条件)或热通量(从中我们可以通过除以边界处的热导率来计算Neumann条件)。类似地,在电学模型中,我们想计算Omegaa中的电压,并知道边界电压(Dirichlet)或这里的(通过电导率潜水后的Neumann条件)。在电气模型中,边界的大部分被电气隔离是很常见的;这是这里的等于零的Neumann边界条件。
最简单的有限元模型将把10兆分为简单的(2D中的三角形,3D中的金字塔)。我们以EIDORS项目中一个带有小型非导电球的圆柱形充液罐为三维示例11该模型旨在反映电阻抗断层扫描的应用,其中将这里的模式应用于这样的储罐,以对内部电导率分布进行成像。为了描述有限元几何,我们有一个垂直矩阵nodes和单纯形elems.
以下示例创建了一个简单的矩形二维电导介质,在相对两侧施加10V和20V(狄利克雷边界条件)。所有其他边缘都进行了电气化处理。
node_y = [1;1.2;1.5;1.8;2]*ones(1,11);
node_x = ones(5,1)*[1,1.05,1.1,1.2, ...
1.3,1.5,1.7,1.8,1.9,1.95,2];
nodes = [node_x(:), node_y(:)];
[h,w] = size (node_x);
elems = [];
for idx = 1:w-1
widx = (idx-1)*h;
elems = [elems; ...
widx+[(1:h-1);(2:h);h+(1:h-1)]'; ...
widx+[(2:h);h+(2:h);h+(1:h-1)]' ];
endfor
E = size (elems,1); # No. of simplices
N = size (nodes,1); # No. of vertices
D = size (elems,2); # dimensions+1
这将创建一个N乘2的矩阵nodes和E-by-3矩阵elems具有定义有限元三角形的值:
nodes(1:7,:)'
1.00 1.00 1.00 1.00 1.00 1.05 1.05 ...
1.00 1.20 1.50 1.80 2.00 1.00 1.20 ...
elems(1:7,:)'
1 2 3 4 2 3 4 ...
2 3 4 5 7 8 9 ...
6 7 8 9 6 7 8 ...
使用一阶有限元法,我们近似了每个单纯形上Omegaas常数的电导率分布(从向量表示conductivity).基于有限元几何,我们首先计算每个单纯形的系统(或刚度)矩阵(在按元系统矩阵的对角线上表示为3乘3个元素)SE). 基于SE和n×DE连接矩阵C,表示单纯形和顶点之间的连接,全局连接矩阵S已计算。
## Element conductivity
conductivity = [1*ones(1,16), ...
2*ones(1,48), 1*ones(1,16)];
## Connectivity matrix
C = sparse ((1:D*E), reshape (elems', ...
D*E, 1), 1, D*E, N);
## Calculate system matrix
Siidx = floor ([0:D*E-1]'/D) * D * ...
ones(1,D) + ones(D*E,1)*(1:D) ;
Sjidx = [1:D*E]'*ones (1,D);
Sdata = zeros (D*E,D);
dfact = factorial (D-1);
for j = 1:E
a = inv ([ones(D,1), ...
nodes(elems(j,:), :)]);
const = conductivity(j) * 2 / ...
dfact / abs (det (a));
Sdata(D*(j-1)+(1:D),:) = const * ...
a(2:D,:)' * a(2:D,:);
endfor
## Element-wise system matrix
SE = sparse(Siidx,Sjidx,Sdata);
## Global system matrix
S = C'* SE *C;
系统矩阵的作用类似于电导率S在欧姆定律中S * V = I基于Dirichlet和Neumann边界条件,我们能够求解每个顶点处的电压V.
## Dirichlet boundary conditions
D_nodes = [1:5, 51:55];
D_value = [10*ones(1,5), 20*ones(1,5)];
V = zeros (N,1);
V(D_nodes) = D_value;
idx = 1:N; # vertices without Dirichlet
# boundary condns
idx(D_nodes) = [];
## Neumann boundary conditions. Note that
## N_value must be normalized by the
## boundary length and element conductivity
N_nodes = [];
N_value = [];
Q = zeros (N,1);
Q(N_nodes) = N_value;
V(idx) = S(idx,idx) \ ( Q(idx) - ...
S(idx,D_nodes) * V(D_nodes));
最后,为了显示解,我们在z轴上显示每个单纯形顶点的每个求解电压值。详见图22.6.
elemx = elems(:,[1,2,3,1])'; xelems = reshape (nodes(elemx, 1), 4, E); yelems = reshape (nodes(elemx, 2), 4, E); velems = reshape (V(elemx), 4, E); plot3 (xelems,yelems,velems,"k"); print "grid.eps";
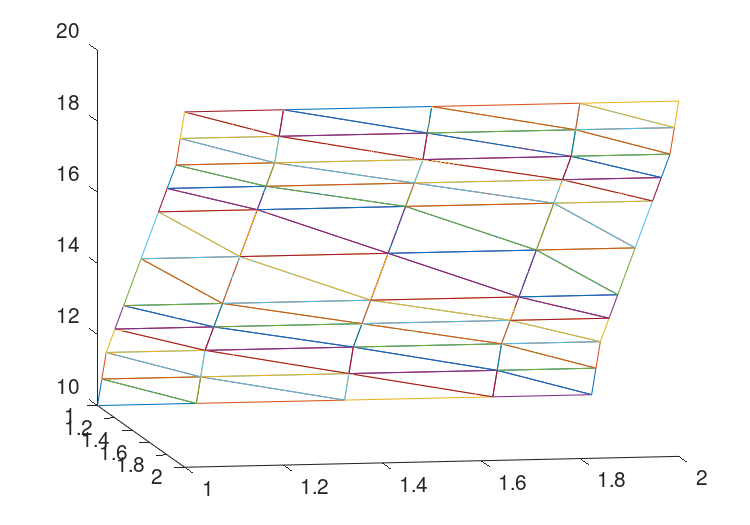
图22.6:示例有限元模型显示三角形单元。每个顶点的高度对应于解的值。