图30.6:从散乱数据到规则网格的插值
Delaunay镶嵌的一个重要用途是,它可以用于将分散的数据插值到任意的点集。要计算已知点集的N单纯形,使用delaunay或delaunayn然后,识别出在其中找到所需点的单形。最后,使用单纯形的顶点来插值到所需的点。执行此插值的函数为griddata, griddata3和griddatan.
zi = griddata (x, y, z, xi, yi) ¶zi = griddata (x, y, z, xi, yi, method) ¶[xi, yi, zi] = griddata (…) ¶vi = griddata (x, y, z, v, xi, yi, zi) ¶vi = griddata (x, y, z, v, xi, yi, zi, method) ¶vi = griddata (x, y, z, v, xi, yi, zi, method, options) ¶在指定点插入不规则的二维和三维源数据。
对于二维插值,输入x和y定义函数所在的点z = f (x, y)评估。输入x, y, z是相同长度的向量,或者是不相等的向量x, y扩展为二维网格meshgrid和z是与X-Y网格的结果大小相匹配的2-D矩阵。
插值点为(xi, yi). 如果且仅当,xi是行向量,并且yi是列向量,则meshgrid将用于创建插值点的网格。
对于三维插值,输入x, y和z定义函数所在的点v = f (x, y, z)评估。输入x, y, z是相同长度的向量,或者如果它们的长度不相等,则将它们扩展为具有meshgrid.输入的大小v必须与原始数据的大小相匹配,无论是向量还是矩阵。
可选的输入插值method可以是"nearest","linear",或用于二维数据"v4"。当方法为"nearest",输出vi将是理论原始数据中最接近的点(x, y, z)到查询点(xi,yi, zi). 当方法为"linear",输出vi将是每个维度中原始源数据中最接近的两个点之间的线性插值。仅对于二维情况"v4"该方法还可以实现双调和样条插值。如果method被省略或为空,默认为"linear".
对于三维插值,可选参数options当计算用于插值的Delaunay三角函数时,直接传递给Qhull。有关默认值以及如何传递不同值的更多信息,详见delaunayn.
编程注意事项:如果输入是复杂的,则实数部分和虚数部分分别进行插值。插值通常基于Delaunay三角函数。输入点凸包之外的任何查询值都将返回NaN。然而"v4"方法不使用三角函数,并且将返回原始数据之外的值(外推)。
vi = griddata3 (x, y, z, v, xi, yi, zi) ¶vi = griddata3 (x, y, z, v, xi, yi, zi, method) ¶vi = griddata3 (x, y, z, v, xi, yi, zi, method, options) ¶在指定点插入不规则的三维源数据。
输入x, y和z定义函数所在的点v = f (x, y, z)评估。Theinputsx, y, z是相同长度的向量,或者是长度不等的向量,则将它们扩展为具有meshgrid.输入的大小v必须匹配理论原始数据的大小,无论是向量还是矩阵。
插值点从指定xi, yi, zi.
可选的输入插值method可以是"nearest"或"linear"。当方法为"nearest",输出vi将是原始数据中最接近的点(x, y, z)到查询点(xi, yi, zi). 当方法为"linear",输出vi将是每个维度中原始源数据中最接近的两个点之间的线性插值。如果method被省略或为空,默认为"linear".
可选参数options在计算用于插值的Delaunay三角函数时,直接传递给Qhull。详见delaunayn有关默认值以及如何传递差值的信息。
编程注意事项:如果输入是复杂的,则实数部分和虚数部分分别进行插值。插值基于Delaunaytriangulation,输入点凸包之外的任何查询值都将返回NaN.
yi = griddatan (x, y, xi) ¶yi = griddatan (x, y, xi, method) ¶yi = griddatan (x, y, xi, method, options) ¶插值不规则源数据x, y在指定的点xi.
输入x是表示N维空间中的M个点的MxN矩阵。输入y是表示在点处评估的函数的单值列向量(Mx1)x即。,y = fcn (x).输入xi是函数输出的点的列表yi应该通过插值来近似。xi必须具有相同数量的列(N像x使得维度匹配。
可选的输入插值method可以是"nearest"或"linear"。当方法为"nearest",输出yi将是原始数据中最接近的点x到查询点xi。当方法为"linear",输出yi将是原始源数据中两个最近点之间的线性插值。如果method被省略或为空,默认为"linear".
可选参数options在计算用于插值的Delaunay三角函数时,直接传递给Qhull。详见delaunayn有关默认值以及如何传递差值的信息。
用例
## Evaluate sombrero() function at irregular data points
x = 16*gallery ("uniformdata", [200,1], 1) - 8;
y = 16*gallery ("uniformdata", [200,1], 11) - 8;
z = sin (sqrt (x.^2 + y.^2)) ./ sqrt (x.^2 + y.^2);
## Create a regular grid and interpolate data
[xi, yi] = ndgrid (linspace (-8, 8, 50));
zi = griddatan ([x, y], z, [xi(:), yi(:)]);
zi = reshape (zi, size (xi));
## Plot results
clf ();
plot3 (x, y, z, "or");
hold on
surf (xi, yi, zi);
legend ("Original Data", "Interpolated Data");
编程注意事项:如果输入是复杂的,则实数部分和虚数部分分别进行插值。插值基于Delaunaytriangulation,输入点凸包之外的任何查询值都将返回NaN。对于二维和三维数据,可以使用griddata作用
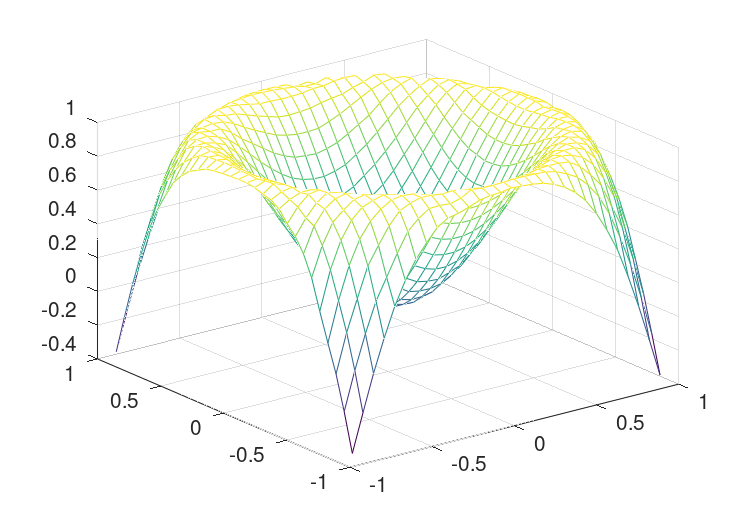
的使用示例griddata函数为
rand ("state", 1);
x = 2*rand (1000,1) - 1;
y = 2*rand (size (x)) - 1;
z = sin (2*(x.^2+y.^2));
[xx,yy] = meshgrid (linspace (-1,1,32));
zz = griddata (x, y, z, xx, yy);
mesh (xx, yy, zz);
从点的随机散射插值到均匀网格。上面的输出可以在中看到图30.6.

图30.6:从散乱数据到规则网格的插值
版权所有 © 2024-2025 Octave中文网
ICP备案/许可证号:黑ICP备2024030411号-2