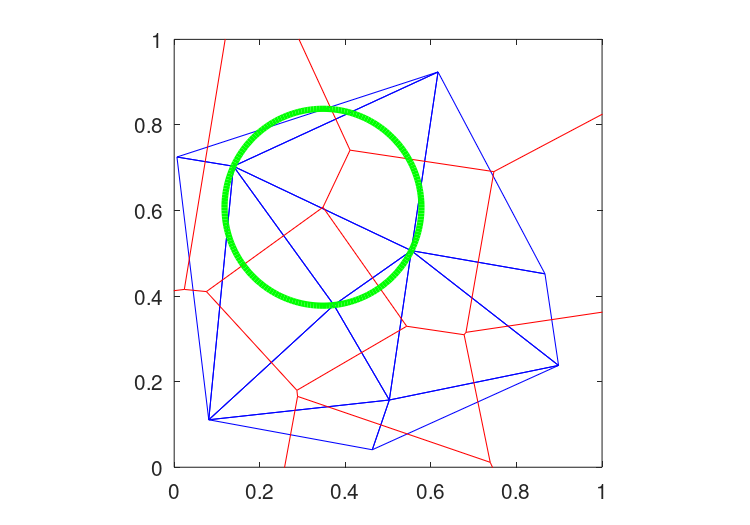
图30.3:随机点集的Delaunay三角函数(蓝线)和Voronoi图(红线)
Voronoi图或点集的Voronoi镶嵌s在N维空间中,是N维空间的镶嵌,使得所有点v(p),其中p是的成员s,更接近p比任何其他点sVoronoi图与一组点的Delaunay三角函数有关,因为Voronois镶嵌的顶点是Delaunay镶嵌的顶点的圆的中心。
(x,y)¶
(x,y,options)¶
(…,“linespec”)¶
(hax, …)¶
h= voronoi (…)¶
[vx,vy] = voronoi (…)¶
绘制点的Voronoi图(x,y).
不绘制点在无穷远处的Voronoi面。
这个options参数必须是字符串或字符串的元胞数组,包含传递给基础qhull命令的参数。有关详细信息,详见Qhull库的文档http://www.qhull.org/html/qh-quick.htm#options.
如果"linespec"它用于设置绘图的颜色和线条样式。
如果轴图形控制柄hax则Voronoi图绘制在指定的轴上,而不是在新的图中。
如果指定单个输出参数,则将绘制Voronoi图和图形句柄h返回到绘图。
[vx,vy]=voronoi(…)返回绘制图表之前的voronoi垂直方向。
x = rand (10, 1);
y = rand (size (x));
h = convhull (x, y);
[vx, vy] = voronoi (x, y);
plot (vx, vy, "-b", x, y, "o", x(h), y(h), "-g");
legend ("", "points", "hull");
[C,F] = voronoin (pts)¶
[C,F] = voronoin (pts,options)¶
计算N维Voronoi面。
输入矩阵pts尺寸为[n,dim]的空间在尺寸为dim的空间中包含n个点。
C包含Voronoi面的点。列表F包含每个方面的Voronoi点的索引。
可选的第二个参数必须是字符串或字符串的元胞数组,其中包含传递给基础qhull命令的参数。有关详细信息,详见Qhull库的文档http://www.qhull.org/html/qh-quick.htm#options.
默认参数取决于输入的尺寸:
{"Qbb"}
{"Qbb", "Qx"}
如果options不存在或[]则使用默认参数。否则options替换默认参数列表。要将用户参数附加到默认值,有必要重复中的默认参数options。使用空字符串不传递任何参数。
的使用示例voronoi是
rand ("state",9);
x = rand (10,1);
y = rand (10,1);
tri = delaunay (x, y);
[vx, vy] = voronoi (x, y, tri);
triplot (tri, x, y, "b");
hold on;
plot (vx, vy, "r");
其结果可以在中看到图30.3请注意,其中一个三角形的循环圆已添加到此图中,以使Delaunay镶嵌和Voronodidiagram之间的关系更加清晰。

图30.3:随机点集的Delaunay三角函数(蓝线)和Voronoi图(红线)
可以通过polyarea和inpolygon函数。
a= polyarea (x,y)¶
a= polyarea (x,y,dim)¶
用三角形法确定多边形的面积。
变量x和y定义顶点对,因此必须具有相同的形状。它们可以是向量,也可以是数组。如果它们是数组,那么的列x和y分别进行治疗,并为每个患者返回一个区域。
如果可选dim给出了参数,那么polyarea沿着数组的这个维度工作x和y.
的使用示例polyarea可能是
rand ("state", 2);
x = rand (10, 1);
y = rand (10, 1);
[c, f] = voronoin ([x, y]);
af = zeros (size (f));
for i = 1 : length (f)
af(i) = polyarea (c (f {i, :}, 1), c (f {i, :}, 2));
endfor
Voronoi图中顶点无穷大的面有无穷大的面积。的简化版本polyarea对于矩形可用rectint
area= rectint (a,b)¶
计算矩形或N-D框的相交面积或体积。
计算中矩形的相交面积a和中的矩形b支持.N维框,在这种情况下,根据维度的数量计算体积或超级体积。
二维矩形定义为[xpos ypos width height]其中xpos和ypos是左下角的位置。在每个维度的最小值的坐标跟随该维度中的框的长度的情况下(例如。,[xpos ypos zpos kpos … width height depth k_length …].
每行a和b定义一个矩形,如果两者都定义了多个矩形,那么输出,area,是一个矩阵,其中第i列对应于a的第i行,第j列对应于b的第j行。
详见: polyarea.
in= inpolygon (x,y,xv,yv)¶
[in,on] = inpolygon (x,y,xv,yv)¶
对于从顶点定义的多边形(xv,yv),如果点为,则返回true(x,y)位于多边形的内部(或边界上);否则,返回false。
输入变量x和y,必须具有相同的维度。
可选输出on如果点正好在多边形边上,则返回true,否则返回false。
详见: delaunay.
的使用示例inpolygon可能是
randn ("state", 2);
x = randn (100, 1);
y = randn (100, 1);
vx = cos (pi * [-1 : 0.1: 1]);
vy = sin (pi * [-1 : 0.1 : 1]);
in = inpolygon (x, y, vx, vy);
plot (vx, vy, x(in), y(in), "r+", x(!in), y(!in), "bo");
axis ([-2, 2, -2, 2]);
其结果可以在中看到图30.4.
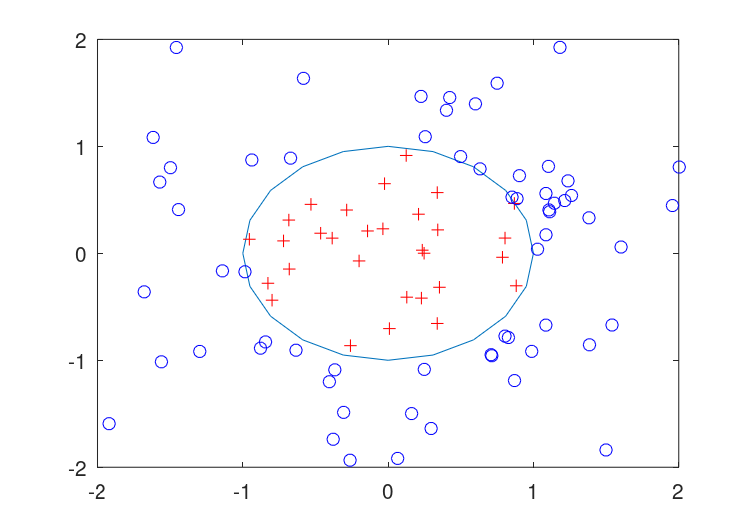
图30.4:的演示inpolygon函数来确定多边形内的点
版权所有 © 2024-2025 Octave中文网
ICP备案/许可证号:黑ICP备2024030411号-2