图30.6:从散乱数据到规则网格的插值
Delaunay镶嵌的一个重要用途是,它可以用于将分散的数据插值到任意的点集。要计算已知点集的N单纯形,使用delaunay或delaunayn然后,识别出在其中找到所需点的单形。最后,使用单纯形的顶点来插值到所需的点。执行此插值的函数为网格, 网格3和网格.
zi = griddata (x, y, z, xi, yi) ¶zi = griddata (x, y, z, xi, yi, method) ¶[xi, yi, zi] = griddata (…) ¶vi = griddata (x, y, z, v, xi, yi, zi) ¶vi = griddata (x, y, z, v, xi, yi, zi, method) ¶vi = griddata (x, y, z, v, xi, yi, zi, method, options) ¶在指定点插入不规则的二维和三维源数据。
对于二维插值,输入x和y定义函数所在的点zfx, y)评估。输入x, y, z是相同长度的向量,或者是不相等的向量x, y扩展为二维网格网格和z是与X-Y网格的结果大小相匹配的2-D矩阵。
插值点为(xi, 易). 如果且仅当,xi是行向量,并且易是列向量,则网格将用于创建插值点的网格。
对于三维插值,输入x, y和z定义函数所在的点vfx, y, z)评估。输入x, y, z是相同长度的向量,或者如果它们的长度不相等,则将它们扩展为具有网格.输入的大小v必须与原始数据的大小相匹配,无论是向量还是矩阵。
可选的输入插值方法可以是最近的,线性的,或用于二维数据v4。当方法为最近的,输出不及物动词将是理论原始数据中最接近的点(x, y, z)到查询点(xi,易, zi). 当方法为线性的,输出不及物动词将是每个维度中原始源数据中最接近的两个点之间的线性插值。仅对于二维情况v4该方法还可以实现双调和样条插值。如果方法被省略或为空,默认为线性的.
对于三维插值,可选参数param当计算用于插值的Delaunay三角函数时,直接传递给Qhull。有关默认值以及如何传递不同值的更多信息,详见delaunayn.
编程注意事项:如果输入是复杂的,则实数部分和虚数部分分别进行插值。插值通常基于Delaunay三角函数。输入点凸包之外的任何查询值都将返回NaN。然而v4方法不使用三角函数,并且将返回原始数据之外的值(外推)。
vi = griddata3 (x, y, z, v, xi, yi, zi) ¶vi = griddata3 (x, y, z, v, xi, yi, zi, method) ¶vi = griddata3 (x, y, z, v, xi, yi, zi, method, options) ¶在指定点插入不规则的三维源数据。
输入x, y和z定义函数所在的点vfx, y, z)评估。Theinputsx, y, z是相同长度的向量,或者是长度不等的向量,则将它们扩展为具有网格.输入的大小v必须匹配理论原始数据的大小,无论是向量还是矩阵。
插值点从指定xi, 易, zi.
可选的输入插值方法可以是最近的或线性的。当方法为最近的,输出不及物动词将是原始数据中最接近的点(x, y, z)到查询点(xi, 易, zi). 当方法为线性的,输出不及物动词将是每个维度中原始源数据中最接近的两个点之间的线性插值。如果方法被省略或为空,默认为线性的.
可选参数param在计算用于插值的Delaunay三角函数时,直接传递给Qhull。详见delaunayn有关默认值以及如何传递差值的信息。
编程注意事项:如果输入是复杂的,则实数部分和虚数部分分别进行插值。插值基于Delaunaytriangulation,输入点凸包之外的任何查询值都将返回NaN.
yi = griddatan (x, y, xi) ¶yi = griddatan (x, y, xi, method) ¶yi = griddatan (x, y, xi, method, options) ¶插值不规则源数据x, y在指定的点xi.
输入x是表示N维空间中的M个点的MxN矩阵。输入y是表示在点处评估的函数的单值列向量(Mx1)x即。,y=fcn(x).输入xi是函数输出的点的列表易应该通过插值来近似。xi必须具有相同数量的列(N像x使得维度匹配。
可选的输入插值方法可以是最近的或线性的。当方法为最近的,输出易将是原始数据中最接近的点x到查询点xi。当方法为线性的,输出易将是原始源数据中两个最近点之间的线性插值。如果方法被省略或为空,默认为线性的.
可选参数param在计算用于插值的Delaunay三角函数时,直接传递给Qhull。详见delaunayn有关默认值以及如何传递差值的信息。
用例
##在不规则数据点处评估sobrero()函数sx=16*gallery(“uniformdata”,[200,1],1)-8;y=16*gallery(“uniformdata”,[200,1],11)-8;z=sin(sqrt(x.^2+y.^2))。/sqrt(x.^2+y.^2);##创建一个规则网格并插入数据[xi,yi]=ndgrid(linspace(-8,8,50));zi=网格([x,y],z,[neneneba xi(:),yi(:)]);zi=整形(zi,大小(xi));##绘图结果sclf();plot3(x,y,z,“或”);坚持冲浪(xi、易、子);图例(“原始数据”、“插值数据”);
编程注意事项:如果输入是复杂的,则实数部分和虚数部分分别进行插值。插值基于Delaunaytriangulation,输入点凸包之外的任何查询值都将返回NaN。对于二维和三维数据,可以使用网格作用
的使用示例网格函数为
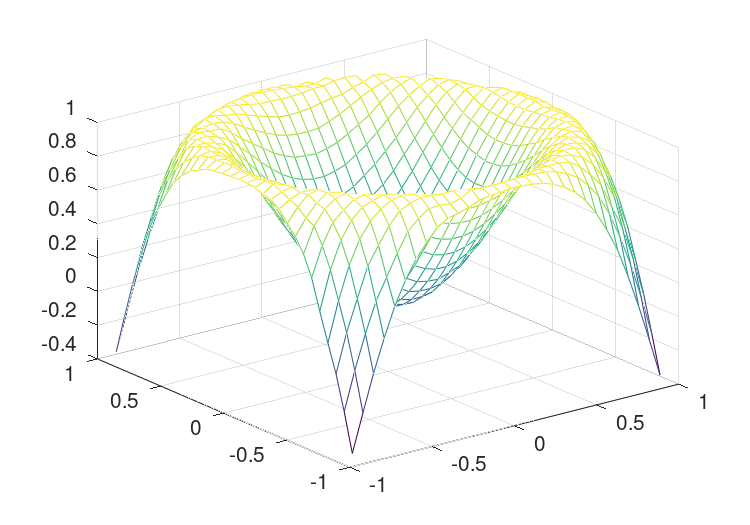
rand(“国家”,1);x=2*rand(1000,1)-1;y=2*rand(大小(x))-1;z=sin(2*(x.^2+y.^2));[xx,yy]=网格(林空间(-1,1,32));zz=网格数据(x,y,z,xx,yy);网格(xx,yy,zz);
从点的随机散射插值到均匀网格。上面的输出可以在中看到图30.6.

图30.6:从散乱数据到规则网格的插值
版权所有 © 2024-2025 Octave中文网
ICP备案/许可证号:黑ICP备2024030411号-2