数学注意事项(GNU Octave(版本10.1.0))

22.1.4.3数学考虑¶

已经尝试使稀疏矩阵以与完全对应矩阵完全相同的方式表现。然而,也有一些不同之处,尤其是与其他产品稀疏实现的不同之处。

首先"./"和".^"运算符必须小心使用。考虑一下这些例子

  s = speye (4);
  a1 = s .^ 2;
  a2 = s .^ s;
  a3 = s .^ -2;
  a4 = s ./ 2;
  a5 = 2 ./ s;
  a6 = s ./ s;

将给予。的第一个示例s被提升到2的幂导致没有问题。然而s就其本身而言,升高的元素涉及大量的术语0 .^ 0即1。那里s .^ s是一个满秩矩阵。

同样地s .^ -2涉及以下术语0 .^ -2哪个是无穷大,所以s .^ -2同样是一个满秩矩阵。

对于“./”运算符s .^ -2没有问题,但是2 ./ s也涉及大量的无穷大项,并且同样是一个满秩矩阵s ./ s涉及以下术语0 ./ 0哪个是NaN所以这同样是一个零元素的满秩矩阵s充满NaN值观

上述行为与满秩矩阵一致,但与其他产品中的稀疏实现不一致。

稀疏矩阵的一个特殊问题是因为零没有被存储,这些零的符号位也同样没有被存储。在某些情况下,零的符号位是重要的。例如

 a = 0 ./ [-1, 1; 1, -1];
 b = 1 ./ a
 ⇒ -Inf            Inf
     Inf           -Inf
 c = 1 ./ sparse (a)
 ⇒  Inf            Inf
     Inf            Inf

要纠正这种行为,就意味着需要将符号位为负的零元素存储在矩阵中,以确保它们的符号位得到查看。因为效率的原因,目前还没有这样做,因此警告用户,在符号位为零很重要的情况下,不能使用稀疏矩阵进行计算。

一般来说,在稀疏矩阵上使用的任何函数或运算符都会导致稀疏矩阵的非零元素数量与原始矩阵相同或更多。这对于稀疏矩阵因子分解的重要情况尤其如此。通常的处理方法是对矩阵进行重新排序,使其因子分解比原始矩阵的因子分解更具解析性L * U = P * S * Q具有更稀疏的项L和U比等价因子分解L * U = S.

根据要分解的矩阵的类型,有几个函数可用于重新排序。如果矩阵是对称正定的,那么symamd或csymmd应该使用。否则amd, colamd或ccolamd应该使用。对于完整性,重新排序函数冷烫和随机排列也可用。

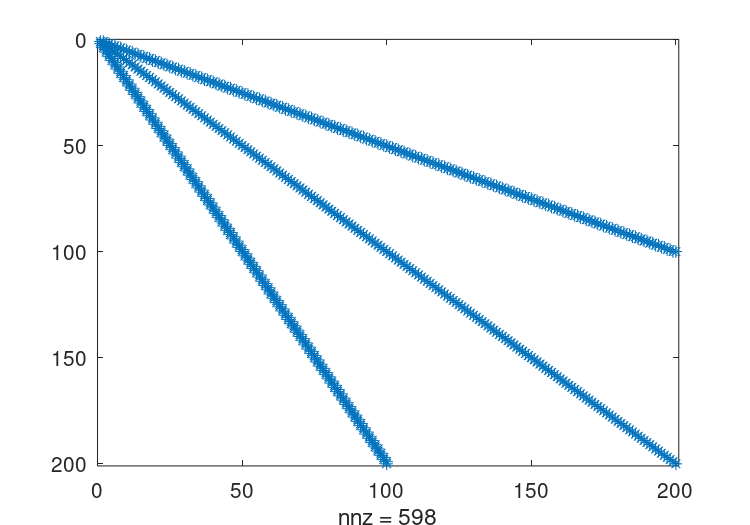
详见图22.3,是一个简单正定矩阵结构体的例子。

图22.3:简单稀疏矩阵的结构体。

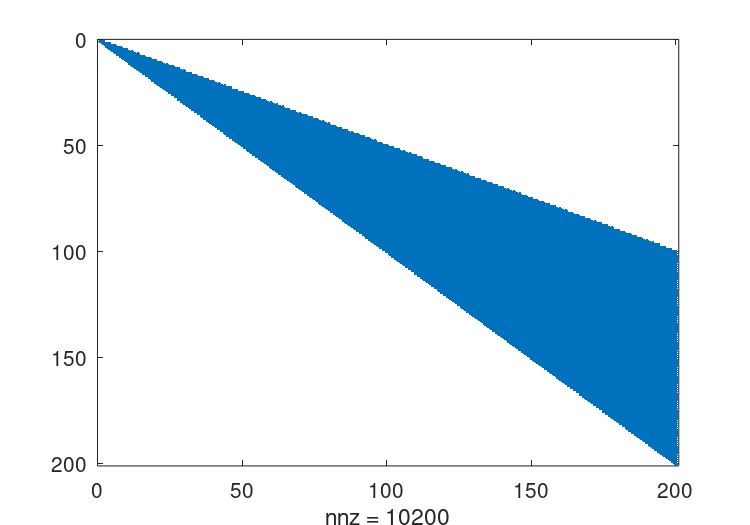
这里的矩阵的标准Cholesky因子分解可以通过与满秩矩阵相同的命令获得r = chol (A); spy (r);详见图22.4原始矩阵有598个非零项,而这种Cholesky因子分解有10200个,只存储了对称矩阵的一半。这是一个重要的填充级别,虽然对于这样一个小的测试用例来说不是问题,但它可以代表与其他稀疏矩阵一起起作用的大量开销。

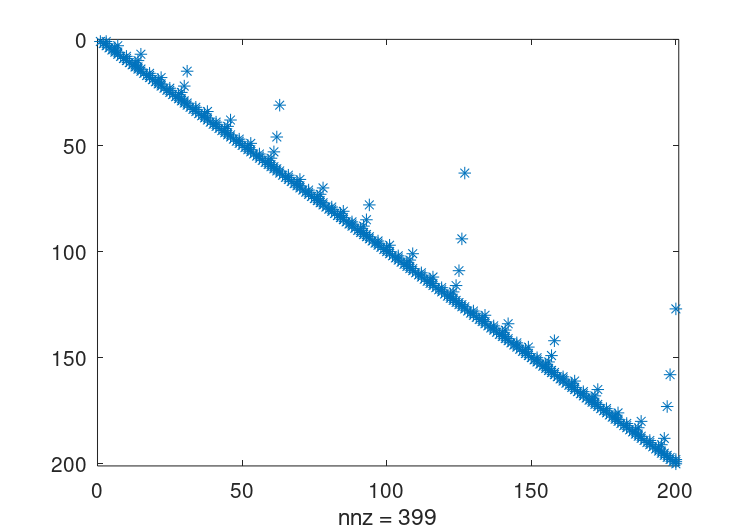
原始矩阵的适当的保稀疏排列从下式给出symamd并且可以使用命令来可视化使用这种重新排序的因子分解q = symamd (A); r = chol (A(q,q)); spy (r)这给出了399个非零项,这是一个显著的改进。

Cholesky因子分解本身可以用于确定在因子分解过程中矩阵的适当的稀疏性保持重排序。在这种情况下,这可以通过三个返回参数获得[r, p, q] = chol (A); spy (r).

图22.4:上述矩阵的非静音Cholesky因子分解的结构体。

图22.5:上述矩阵的置换Cholesky因子分解的结构体。

在非对称矩阵的情况下,适当的保稀疏排列是colamd使用这种重新排序的因子分解可以使用命令进行可视化q = colamd (A); [l, u, p] = lu (A(:,q)); spy (l+u).

最后,当使用div(/)和ldiv(\)运算符时,Octave隐式地重新排序矩阵,因此用户不需要显式地重新排列矩阵以最大限度地提高性能。

: p = amd (S) ¶

: p = amd (S, opts) ¶

返回矩阵的近似最小阶置换。

这是一个置换,使得的Cholesky因子分解S (p, p)往往比的Holesky因子分解更稀疏S它本身amd通常比symamd但具有类似的目的。

可选参数opts是一个控制行为的结构体amd。该结构体的字段为

opts.dense: 确定什么amd认为是输入矩阵的密集行或列。超过的行或列max (16, (dense * sqrt (n)))分量,其中n是矩阵的顺序S,被忽略amd在排列的计算期间。稠密的值必须是正标量,默认值为10.0